Predicativity: The Outer Limits
Stephen G. Simpson
Abstract
Beginning with ideas of Poincaré and Weyl, Feferman in the sixties
undertook a profound analysis of the predicativist foundational program. He
presented a subystem of second order arithmetic
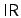 and
argued convincingly that it represents the outer limits of what is
predicatively provable. Much later, Friedman introduced another
system
and
argued convincingly that it represents the outer limits of what is
predicatively provable. Much later, Friedman introduced another
system
 which is conservative over
which is conservative over
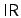 for
for
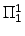 sentences yet includes several well known theorems of
algebra, descriptive set theory, and countable combinatorics that are
not provable in
sentences yet includes several well known theorems of
algebra, descriptive set theory, and countable combinatorics that are
not provable in
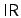 .
The proof-theoretic ordinal of both
systems is
.
The proof-theoretic ordinal of both
systems is 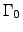 .
.
 has emerged as one of a
handful of systems that are important for reverse mathematics. From a
foundational standpoint, we may say that
has emerged as one of a
handful of systems that are important for reverse mathematics. From a
foundational standpoint, we may say that
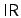 represents
predicative provability while
represents
predicative provability while
 represents predicative
reducibility. Subsequently Friedman formulated mathematically natural
finite combinatorial theorems that are not only not predicatively
provable but go beyond
represents predicative
reducibility. Subsequently Friedman formulated mathematically natural
finite combinatorial theorems that are not only not predicatively
provable but go beyond 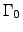 and therefore are not predicatively
reducible. I plan to report on recent developments in this area.
and therefore are not predicatively
reducible. I plan to report on recent developments in this area.