Another well known result of Ramsey theory is Van der Waerden's theorem:
IfUsing a method of Shelah, Van der Waerden's theorem is known to be provable inis colored with finitely many colors, then one of the colors contains arithmetic progressions of arbitrary finite length.
IfEssentially nothing is known about the strength of Szemerédi's theorem. In particular it is unknown whether Szemerédi's theorem is provable inis such that
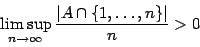
then A contains arithmetic progressions of arbitrary finite length.