Real Analysis and Topology

Much is known concerning reverse mathematics for real analysis and the topology of complete separable metric spaces. Some of the inspiration for this comes from recursive analysis [25] and Bishop-style constructivism [2]. We shall not discuss those connections here, but see my book [32] for more information.

In Giusto/Simpson [11] we presented a rather thorough reverse mathematics discussion of various notions of closed set, and of various forms of the Tietze extension theorem for real-valued continuous functions on closed sets, in compact metric spaces. The purpose of this section is to call attention to one open problem left over from that paper.

Let X be a compact metric space. For concreteness we may take X=[0,1], the unit interval. In $\mathsf{RCA}_0$ we define $K\subseteq X$ to be closed if it is the complement of a sequence of open balls; separably closed if it is the closure of a sequence of points; located if the distance function d(x,K) exists as a continuous real-valued function on X; weakly located if the predicate d(x,K)>r is $\Sigma^0_1$ (allowing parameters, of course). C(X) denotes the separable Banach space of continuous real-valued functions on X which have a modulus of uniform continuity. The strong Tietze theorem for K is the statement that every $\phi\in\mathrm{C}(K)$ extends to some $\widetilde{\phi}\in\mathrm{C}(X)$. See [11] for details.

Known results from [11] are:

(1)

The strong Tietze theorem for closed, weakly located sets is provable in $\mathsf{RCA}_0$.

(2)

The strong Tietze theorem for separably closed sets is equivalent to $\mathsf{WKL}_0$ over $\mathsf{RCA}_0$.

There remain open questions concerning the status of

(3)

the strong Tietze theorem for closed sets, and

(4)

the strong Tietze theorem for closed, separably closed sets.

It is known from [11] that (3) and (4) are provable in $\mathsf{WKL}_0$and not provable in $\mathsf{RCA}_0$. There is a partial reversal: (3) or (4) implies the DNR axiom over $\mathsf{RCA}_0$. We shall outline the proof of this below. But first we discuss the DNR axiom.

The DNR axiom says: For every $A\subseteq\mathbb{N}$ there exists $f:\mathbb{N}\to\mathbb{N}$ which is diagonally nonrecursive relative to A, i.e., $f(n)\ne\{n\}^A(n)$ for all $n\in\mathbb{N}$. Here $\mathbb{N}$ is the set of natural numbers. It would be possible to restate the DNR axiom in a combinatorial way, not involving recursion theory, but we shall not do so here.

The DNR axiom is known to be weaker than $\mathsf{WKL}_0$ ( $=\mathsf{RCA}_0\,\,+$ weak König's lemma). Indeed, the DNR axiom is provable in the strictly weaker system $\mathsf{WWKL}_0$ ( ${}=\mathsf{RCA}_0+{}$ weak weak König's lemma) which arises in connection with reverse mathematics for measure theory. (See [32, §X.1], [11], [4].) Because of Kumabe's result [21], it seems likely that the DNR axiom is strictly weaker than $\mathsf{WWKL}_0$.

Recursion theorists can understand these variants of weak König's lemma in terms of separating sets, recursively bounded $\Pi^0_1$classes, etc. Thus there is a close connection with Jockusch's talk at this conference. In descending order we have:

1.

$\mathsf{WKL}_0$ is just $\mathsf{RCA}_0$ plus any of the following, relativized to arbitrary $A\subseteq\mathbb{N}$:

(a)

for every infinite recursive tree $T\subseteq\{0,1\}^{<\mathbb{N} }$, there exists a path through T.

(b)

for every disjoint pair of r.e. sets, there exists a separating set.

(c)

there exists a $\{0,1\}$-valued DNR function, i.e., a function $f:\mathbb{N}\to\{0,1\}$ such that $f(n)\ne\{n\}(n)$ for all $n\in\mathbb{N}$.

2.

$\mathsf{WWKL}_0$ is just $\mathsf{RCA}_0$ plus either of the following, relativized to arbitrary $A\subseteq\mathbb{N}$:

(a)

for every recursive tree $T\subseteq\{0,1\}^{<\mathbb{N} }$ such that

$$\lim_n\frac{\vert\{\sigma\in T:\mathrm{lh}(\sigma)=n\}\vert}{2^n}\ne0$$

there exists a path through T.

(b)

there exists a 1-random real (see Kucera [18,19,20]).

3.

The DNR axiom is equivalent over $\mathsf{RCA}_0$ to the following, relativized to arbitrary $A\subseteq\mathbb{N}$:

(a)

there exists a DNR function, i.e., a function $f:\mathbb{N}\to\mathbb{N}$ such that $f(n)\ne\{n\}(n)$ for all $n\in\mathbb{N}$.

Unfortunately, we don't know much about how to use the DNR axiom in mathematical arguments. Unlike $\mathsf{WKL}_0$ and $\mathsf{WWKL}_0$, the DNR axiom seems weak and therefore difficult to apply.

We shall now end this section with an outline of the proof that the strong Tietze theorem for closed, separably closed subsets of [0,1]implies the DNR axiom.

We may as well assume that weak König's lemma fails. For each nlet I_n be the closed interval [1/2²ⁿ⁺¹,1/2²ⁿ]. Since weak König's lemma fails, the Heine/Borel covering lemma fails, so let (a_nk,b_nk), $k\in\mathbb{N}$, be a covering of I_n by open intervals with no finite subcovering. We may assume that these coverings are disjoint from one other.

If $\{n\}(n)$ is defined, let s_n be the least s such that $\{n\}_s(n)$ is defined, and put

$$J_n=I_n\setminus\bigcup_{k=0}^{s_n}(a_{nk},b_{nk}).$$

Let

$$K=\{0\}\cup\bigcup\{J_n:\{n\}(n)\mbox{ is defined}\}.$$

It can be shown that $K\subseteq[0,1]$ is closed, separably closed, and not weakly located.

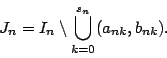
Define a real-valued continuous function $\phi(x)=\pm x$ on K, as follows. First let p_i(x), $i\in\mathbb{N}$, be a fixed, one-to-one, recursive enumeration of $\mathbb{Q} [x]$, the ring of polynomials with rational coefficients in one indeterminate, x. Using this, define $\phi(0)=0$ and, for $\{n\}(n)=i$ and $x\in J_n$, $\phi(x)=x$ if $\vert p_i(z)-z\vert\ge1/2^{2n+2}$ for some $z\in J_n$, $\phi(x)=-x$ otherwise. It can be shown that $\phi\in\mathrm{C}(K)$.

By the strong Tietze theorem for K, let $\widetilde{\phi}\in\mathrm{C}([0,1])$ be an extension of $\phi$ from K to all of [0,1]. By Weierstrass polynomial approximation in $\mathsf{RCA}_0$, let p_in(x), $n\in\mathbb{N}$, be a sequence of polynomials such that $\sup\{\vert\widetilde{\phi}(x)-p_{i_n}(x)\vert:0\le x\le1\}<1/2^{2n+2}$ for all n. It is not difficult to show that the function $f:\mathbb{N}\to\mathbb{N}$ given by f(n)=i_n is DNR.

By relativizing the above to an arbitrary $A\subseteq\mathbb{N}$, we get a function that is DNR relative to A. This completes the proof.

Note: Recursion theorists may want to view the above as a standard diagonal construction leading to a recursive counterexample to (4). However, from the viewpoint of reverse mathematics, there seems to be something unusual going on here. Usually, a recursive counterexample leads to a reversal to $\mathsf{ACA}_0$ or $\mathsf{WKL}_0$, but in this instance all we seem to get is a reversal to the DNR axiom.