John P. Burgess
Department of Philosophy
Princeton
University
Princeton NJ 08544
October 22, 1999
It is the norm rather than the exception for a field within mathematics that originated with certain kinds of applications in mind to steer or drift away from them in its subsequent development, as specialists become interested in other applications, or connections with core mathematics, or pure theory. Though mathematical logic has never quite won acceptance in mathematics departments as a normal branch of mathematics, its development has been entirely normal in the respect just indicated. It is now unfortunately a comparatively rare event for a book to be published in the field that has any very direct application to or connection with the kinds of philosophical issues that concerned the field's originators. Indeed, it is a rare enough event to make it appropriate for a philosophical journal to take note of the appearance of such a book, even if detailed discussion of its technical content would be beyond the scope of the journal.
The book under review is one of these rare exceptions. The author has generously made the first chapter, which contains among other things an outline of the whole book, available by posting it on the web1. The site also contains links to other materials related to the book, including a short account of developments in the field since the book appeared. The availability of this resource, will I hope excuse me from dealing with some of the more technical aspects of the work, which in any case might not be appropriate in this journal, and allow me to concentrate on philosophical issues.
The philosophical issues to which the book's results are relevant are those raised by the existence of sects of heretical mathematicians who on one or another philosophical or ideological ground have rejected many of the proofs offered by their orthodox colleagues, and have insisted on a different and generally speaking more restrictive notion of what constitutes a genuine proof whose conclusions may be accepted as meaningful and true. (The best known of the heretics was L. E. J. Brouwer, founder of intuitionism, which rejects not only many of the axioms from which orthodox proofs proceed, but also many of the rules of logic by which those proofs proceed.)
Such heresies are of interest philosophically from two points of view. On the one hand, there are philosophers who think the question of what are the appropriate axioms and rules of logic for mathematics to be one that it is appropriate and important for philosophers to address, and among the philosophers in this first group there are many who actually sympathize with the heretics. (The best known presentday example is Michael Dummett, a strong sympathizer with intuitionism.)
On the other hand, there are philosophers who think it is no part of the philosopher's business to dictate to mathematicians what methods they may or may not use. For them, perhaps the most central question to what extent has mathematics as we know it been shaped by mathematical facts independent of us, and to what extent by ``anthropological'' facts about us? For them the question of how much mathematics could be developed (and especially the question whether enough mathematics for purposes of scientific applications could be developed) on some more restricted basis than current orthodoxy is of interest for its bearing on the question of far orthodox mathematics was forced upon us, and how far its current acceptance was the result of psychological and sociological and historical contingencies.
Mathematical logic provides mathematical tools for studying questions about how many and just which results would or would not have been available if the choice of axioms or rules of logic had been different. Like any other branch of applied mathematics, philosophically-oriented mathematical logic, also called foundational studies (though to philosophers this label may misleadingly tend to suggest that its practitioners are committed to a ``foundationalist'' epistemology, which need not be the case), proposes an idealized mathematical representation of the phenomenon under study and proves mathematical results about the idealized mathematical respresentation, which then suggest conclusions about the phenomenon of interest. In this case, the phenomenon of interest is mathematical provability, by orthodox or heterodox standards, and the idealized mathematical reprsentations are formal systems.
It is not claimed in foundational studies that proofs in a formal system closely resemble what an ordinary working mathematician would call a ``proof'', any more than it is claimed in recursion theory that computations on a Turing machine closely resemble what an ordinary working mathematician would call a ``computation''. It is provability and computability that is being represented, rather than proof or computation as such, and what is claimed in the one case is that whenever there is a what an ordinary working mathematician would call a ``proof'' there is a proof in a relevant formal system, just as what is claimed in the other case is that whenever there is what an ordinary working mathematician would call a ``computation'' there is a computation on a Turing machine. The latter claim is known as Turing's thesis, and the former is sometimes called Hilbert's thesis.
For orthodox mathematics as a whole, the best formal idealization is
provided by a system of axiomatic set theory such as the one called
![]() .
For the non-set-theoretic mathematics (``that body of
mathematics which is prior to and independent of abstract
set-theoretic concepts'' as contrasted with ``those branches of
mathematics that were created by the set-theoretic revolution that
took place approximately a century ago'', in the words of the book
under review), David Hilbert and Paul Bernays long ago proposed a
formal idealization named ``second-order arithmetic''.
.
For the non-set-theoretic mathematics (``that body of
mathematics which is prior to and independent of abstract
set-theoretic concepts'' as contrasted with ``those branches of
mathematics that were created by the set-theoretic revolution that
took place approximately a century ago'', in the words of the book
under review), David Hilbert and Paul Bernays long ago proposed a
formal idealization named ``second-order arithmetic''.
Philosophers who have heard of ``second-order logic'' may be in some
danger of being misled by this name. Forget all about ``second-order
logic'' and ``second-order theories'' in the sense of sets of
sentences of a formal language that are closed under some second-order
consequence relation. The formal system
![]() called ``second-order
arithmetic'' is a first-order theory, though one with two kinds
of variables, number variables
called ``second-order
arithmetic'' is a first-order theory, though one with two kinds
of variables, number variables
![]() and set variables
and set variables
![]() ,
having in addition to symbols of the basic relations
and operations on natural numbers the symbol
,
having in addition to symbols of the basic relations
and operations on natural numbers the symbol ![]() for membership of a
number in a set of numbers. It has a few basic axioms about the basic
relations and operations, plus two further items.
for membership of a
number in a set of numbers. It has a few basic axioms about the basic
relations and operations, plus two further items.
First, there is the axiom of induction:
![]() as such deals with only two kinds of
mathematical objects, natural numbers and sets thereof.
However, the usual set-theoretic proofs that, say, there are
no more rational numbers than natural numbers, and no
more real numbers than sets of natural numbers, actually
show how to ``code'' rational numbers by natural numbers,
and real numbers by sets of natural numbers, and it is
possible, therefore to express theorems about rational and
real numbers and many other kinds of mathematical objects
in ``coded'' form in the language of
as such deals with only two kinds of
mathematical objects, natural numbers and sets thereof.
However, the usual set-theoretic proofs that, say, there are
no more rational numbers than natural numbers, and no
more real numbers than sets of natural numbers, actually
show how to ``code'' rational numbers by natural numbers,
and real numbers by sets of natural numbers, and it is
possible, therefore to express theorems about rational and
real numbers and many other kinds of mathematical objects
in ``coded'' form in the language of
![]() .
(There are
actually many different codings for each kind of
mathematical object. The question of why the particular
codings used in the book under review are more appropriate
than others is touched on only briefly in the book.)
.
(There are
actually many different codings for each kind of
mathematical object. The question of why the particular
codings used in the book under review are more appropriate
than others is touched on only briefly in the book.)
The ``subsystems'' of the book's title all differ from the full
second-order arithmetic (only) by involving weaker assumptions on
set-existence than the full comprehension scheme. Five subsystems,
which in order of increasing strength may be called S1 through S5(and are officially named
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() -
-
![]() ), are intensively studied in the book. In three of
them, the set-existence assumptions are simply comprehension for
formulas of a suitably restricted kind.
), are intensively studied in the book. In three of
them, the set-existence assumptions are simply comprehension for
formulas of a suitably restricted kind.
The simplest class of formulas are those that involve no
quantifications over numbers and only bounded quantifications
![]() or
or
![]() ,
abbreviated
,
abbreviated
![]() and
and
![]() .
These may be called
bounded formulas. More complex are formulas of the types
.
These may be called
bounded formulas. More complex are formulas of the types
![]() and
and
![]() where
where ![]() is bounded.
These are called
is bounded.
These are called ![]() and
and
![]() formulas. Whether or not
a bounded formula
formulas. Whether or not
a bounded formula
![]() is correct for particular
numerical values of
is correct for particular
numerical values of ![]() can always be effectively decided by a
computation, and any such numerical instance can always be proved if
correct and disproved if incorrect, even in the weakest of the systems
considered in the book, by exhibiting a formalized version of the
relevant computation. Likewise, any correct
can always be effectively decided by a
computation, and any such numerical instance can always be proved if
correct and disproved if incorrect, even in the weakest of the systems
considered in the book, by exhibiting a formalized version of the
relevant computation. Likewise, any correct
![]() formula can
be proved, by proving a correct numerical instance, and any incorrect
formula can
be proved, by proving a correct numerical instance, and any incorrect
![]() formula can be disproved by disproving an incorrect
numerical instance. More complex are formulas of the types
formula can be disproved by disproving an incorrect
numerical instance. More complex are formulas of the types
![]() and
and
![]() with
with ![]() bounded. These are called
bounded. These are called ![]() and
and
![]() formulas. More
generally, formulas involving as many quantifications over numbers as
desired, but no quantification over sets, are called
arithmetical formulas. More complex are formulas of the types
formulas. More
generally, formulas involving as many quantifications over numbers as
desired, but no quantification over sets, are called
arithmetical formulas. More complex are formulas of the types
![]() and
and
![]() where
where ![]() is arithmetical. These
are called
is arithmetical. These
are called ![]() and
and
![]() formulas.
formulas.
The base system S1 provides only for the existence
of recursive sets of natural numbers. For any such set, the
set itself can be defined by a
![]() formula
formula
![]() and its complement can be defined
by a different
and its complement can be defined
by a different
![]() formula
formula
![]() .
(This is one of the lemmas proved in intermediate-level logic
courses on the way to the proof of the Gödel
incompleteness theorems.) The set-existence axiom for S1 therefore
takes the form:
.
(This is one of the lemmas proved in intermediate-level logic
courses on the way to the proof of the Gödel
incompleteness theorems.) The set-existence axiom for S1 therefore
takes the form:
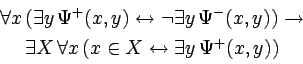
The systems S2 and S4, whose significance was first appreciated
by Harvey Friedman, who may be considered the originator of the branch
of logical studies of which the author of the book under review has
been the principal developer, are different. Each admits of several
equivalent formulation. For S2, one may take the set-existence
axioms to be of the following form, wherein ![]() and
and ![]() are bounded:
are bounded:
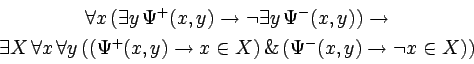
It should be emphasized that S1, say, is not a formal
system of ``recursive mathematics'' in the sense of a formal
system of mathematics in which it is assumed that only
recursive sets exist. Rather, S1 assumes the existence
of recursive sets, and does not assume anything one way or
the other about the existence of non-recursive sets. In
proving an existential statement, one can only prove
![]() by proving that there is a recursive set X
with the property expressed by the formula
by proving that there is a recursive set X
with the property expressed by the formula ![]() .
But in
proving a universal statement,
.
But in
proving a universal statement,
![]() ,
no use is
made of any axiom to the effect that the only X that need be
considered are recursive. There is no such axiom in the
system, and a proof of a universal statement in the system
really does constitute an orthodox proof that all sets X of
natural numbers, not just the recursive ones, have the
property expressed by the formula
,
no use is
made of any axiom to the effect that the only X that need be
considered are recursive. There is no such axiom in the
system, and a proof of a universal statement in the system
really does constitute an orthodox proof that all sets X of
natural numbers, not just the recursive ones, have the
property expressed by the formula ![]() .
The system S1
(and this goes for the other systems Si also) is a
subsystem of orthodox second-order arithmetic
.
The system S1
(and this goes for the other systems Si also) is a
subsystem of orthodox second-order arithmetic
![]() and
has no theorems that contradict theorems of orthodox
mathematics. (By contrast, intuitionistic mathematics
notoriously does have such anti-classical theorems.)
and
has no theorems that contradict theorems of orthodox
mathematics. (By contrast, intuitionistic mathematics
notoriously does have such anti-classical theorems.)
There are also formal systems that codify various restrictive,
heterodox forms of mathematics, among which four may be mentioned in
order of increasing strength:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
which for present purposes I will call T2 through T5. The
heresies or 'isms they codify may be called finitism,
intuitionism minus choice sequences, predicativism, and
predicativism plus inductive definitions. (Intuitionism proper
does not appear on the list: Brouwer's thought resists full
formalization, and if one took fully seriously his doctrine of the
``creative subject'', intuitionistic second-order arithmetic would be
a system equivalent in strength to orthodox second-order arithmetic
,
which for present purposes I will call T2 through T5. The
heresies or 'isms they codify may be called finitism,
intuitionism minus choice sequences, predicativism, and
predicativism plus inductive definitions. (Intuitionism proper
does not appear on the list: Brouwer's thought resists full
formalization, and if one took fully seriously his doctrine of the
``creative subject'', intuitionistic second-order arithmetic would be
a system equivalent in strength to orthodox second-order arithmetic
![]() .)
.)
The book under review has two parts. The first part of the book is devoted to showing how and how far various branches of non-set-theoretic mathematics can be developed in one or another of the systems Si. Algebra and analysis (the branch of mathematics whose most basic part is differential and integral calculus) are treated in some detail, and the results covered in the book and the related papers cited at the end take one to the threshhold of the kind of higher analysis used, for instance, in the mathematical treatment of quantum mechanics.
A characteristic phenomenon encountered is that when some theorem
![]() is proved in a system Si+1 and resists proof in the next
lower system Si, it often turns out that in fact adding the theorem
is proved in a system Si+1 and resists proof in the next
lower system Si, it often turns out that in fact adding the theorem
![]() to the axioms of the base system S1 actually would enable
one to prove the characteristic axioms of Si+1. Such proving of
axioms from theorems is called ``reverse mathematics'', and is a main
theme of the first part of the book.
to the axioms of the base system S1 actually would enable
one to prove the characteristic axioms of Si+1. Such proving of
axioms from theorems is called ``reverse mathematics'', and is a main
theme of the first part of the book.
The second part of the book is devoted to the study of models of the
Si in the sense of the branch of mathematical logic known as
``formal semantics'' or ``model theory''. It culminates in a in
``semantic'' or ``model-theoretic'' proofs of conservativeness
results, which in general have the form: ``Every formula of
such-and-such a degree of complexity that is provable in such-and-such
a subsystem S of
![]() is actually provably in such-and-such a
formal system T intended to codify such-and-such a restricted,
heterodox form of mathematics.'' The main such results -- the book
includes proofs of some and references to the literature where proofs
for the others may be found -- are the conservativeness of Si over
Ti for
is actually provably in such-and-such a
formal system T intended to codify such-and-such a restricted,
heterodox form of mathematics.'' The main such results -- the book
includes proofs of some and references to the literature where proofs
for the others may be found -- are the conservativeness of Si over
Ti for ![]() in the case of i = 2 or 3, and for
in the case of i = 2 or 3, and for ![]() formulas in the case of i = 4 or 5. There are also ``syntactic''
or ``proof-theoretic'' proofs of such theorems.
formulas in the case of i = 4 or 5. There are also ``syntactic''
or ``proof-theoretic'' proofs of such theorems.
Together the results of the two parts of the book show that the various heresies or 'isms ``correspond'' in a sense to natural distinctions that can be made within orthodox mathematics, pertaining to the strength of set-theoretic axioms used -- and by ``reverse mathematics'' unavoidably used -- to prove various theorems.
There are various ways in which one might wish to see the program represented by the book extended. For instance, geometry in general, and the kind of higher geometry used in the mathematical treatment of general relativity in particular, has not yet been treated as fully as algebra and analysis -- not indeed that there aren't plenty of subbranches of algebra and analysis the strength of whose set-theoretic presuppositions remain to be calibrated by another generation of students.
Also, to facilitate comparison with the actual productions of ordinary, working mathematicians, and to reduce the need for coding and particular choices of codings, it would be desirable to develop a more flexible formalism that permitted one to talk directly about sets of sets of natural numbers, for instance. The trouble here is that as soon as one admits such ``higher-order'' objects one faces a labyrinth of options as to how to treat them, and in the literature where such matters are considered, no particular format seems yet to have emerged as optimal.
One might also consider looking for stronger systems S6, S7,
...that would in some natural way continue the series S1 through
S5, and there is in fact some discussion of stronger systems in the
book. Results statable in the language of
![]() that are not
provable in S5 exist, as do results so statable that are not
provable in full
that are not
provable in S5 exist, as do results so statable that are not
provable in full
![]() ,
as do results so statable that are not
provable even in
,
as do results so statable that are not
provable even in
![]() but that become provable with the additional
assumption of ``large cardinal'' axioms. But these are few and far
between. Inversely, since there are heresies or 'isms more
restrictive even than finitism, one might consider looking for a
weaker system S0 to ``correspond'' to the most important of them.
In fact, some first steps towards weakening the base theory are
reported in the book.
but that become provable with the additional
assumption of ``large cardinal'' axioms. But these are few and far
between. Inversely, since there are heresies or 'isms more
restrictive even than finitism, one might consider looking for a
weaker system S0 to ``correspond'' to the most important of them.
In fact, some first steps towards weakening the base theory are
reported in the book.
It is all too easy for the philosopher to raise a whole series of questions the answering of anyone of which would call for a great deal of labor on the part of the logician, so let me stop here, emphasizing that the remark that there may be more work to be done is no criticism of the work that has been done. On the contrary, it is an important virtue in a book to raise new questions even while answering old ones, and the book under review possesses this virtue to a high degree.
If there is any point on which I do have a reservation, it is on the author's discussion of ``Hilbert's program'', and even here, any criticism must be tempered by a recognition aim of the book is to present results of mathematical logic that have bearing on philosophical concerns, rather than to spell out in detail what that bearing is. This makes it almost inevitable that such digressions as there are on philosophical topics will be rather compressed and incomplete.
Bearing this in mind, my concern is as follows. Hilbert's idea was to
try to persuade the finitists, who considered most of orthodox
mathematics meaningless, to abandon their opposition to orthodox
mathematics, by convincing them that whenever there is an orthodox
proof of a theorem of the limited class they considered meaningful,
the result will be true because there will be a finitist proof of it.
In jargon, the ambition was roughly to prove
![]() conservative over
conservative over
![]() for
for ![]() formulas at least. Gödel's
incompleteness theorems imply that
formulas at least. Gödel's
incompleteness theorems imply that
![]() simply is not thus
conservative over
simply is not thus
conservative over
![]() .
Results in the book under review imply that
.
Results in the book under review imply that
![]() is. Do we have here, as the author claims, a partial
realization of Hilbert's program?
is. Do we have here, as the author claims, a partial
realization of Hilbert's program?
My answer would be, not yet, not so long as we have only given only an
orthodox proof of the conservativeness theorem (or only give an
orthodox proof that there must exist a finitist proof of the
conservativeness theorem); but yes, as soon as we give a finitist
proof of the conservativeness theorem (and even if we only just give a
finitist proof that there must be a finitist proof of the
conservativeness theorem). To argue that the finitist should accept a
given
![]() theorem because there is a proof of it in
theorem because there is a proof of it in
![]() ,
and a proof in
,
and a proof in
![]() that if there is a proof of it in
that if there is a proof of it in
![]() ,
then
there is a proof of it in
,
then
there is a proof of it in
![]() ,
is rather like arguing that an
atheist should accept some given doctrine on the grounds that the pope
has proclaimed it, and that the pope has proclaimed that his doctrinal
pronouncements are infallible.
,
is rather like arguing that an
atheist should accept some given doctrine on the grounds that the pope
has proclaimed it, and that the pope has proclaimed that his doctrinal
pronouncements are infallible.
The author's discussion in the book does not make this distinction very clear. In practice, ``semantic'' or ``model-theoretic'' proofs generally are not finitist as they stand, while ``syntactic'' or ``proof-theoretic'' proofs generally are finitist; but model-theoretic proofs can often be turned into finitist ones after the fact, so to speak, by some clever trick. In the present case, the trick was performed some years ago by Harvey Friedman, but he has only just recently (since the appearance of Simpson's book) written it up for electronic posting (with a link on Simpson's site mentioned above), and it has not yet appeared in print.
But this is a rather picayune complaint given how many matters that are clarified. I am tempted to say that everyone interested in philosophy of mathematics should read this book, but hesistate since not everyone with such an interest will have the requisite technical background to work through the book, and even trained logicians will find parts of it a challenge. What I will say is that everyone interested in philosophy of mathematics who has the requisite training in logic should tackle this book, and everyone with an interest in philosophy of mathematics, even if their primary interest is not in the technical side of the subject, should be aware of its contents.